Mapping Images to Images

Many problems in image processing, graphics, and vision involve transforming an input image into a corresponding output image. There exist a wide variety of domain specific solutions for many problems—Colorization, Edge Detection, Segmentation, Neural Style Transfer, etc.—even though the goal is always the same: mapping pixels to pixels.
One obvious question we can ask is: does there exist a general-purpose solution to this problem? That is, given two paired domains of images $X$ and $Y$, can we always find a function $G : X \rightarrow Y$?
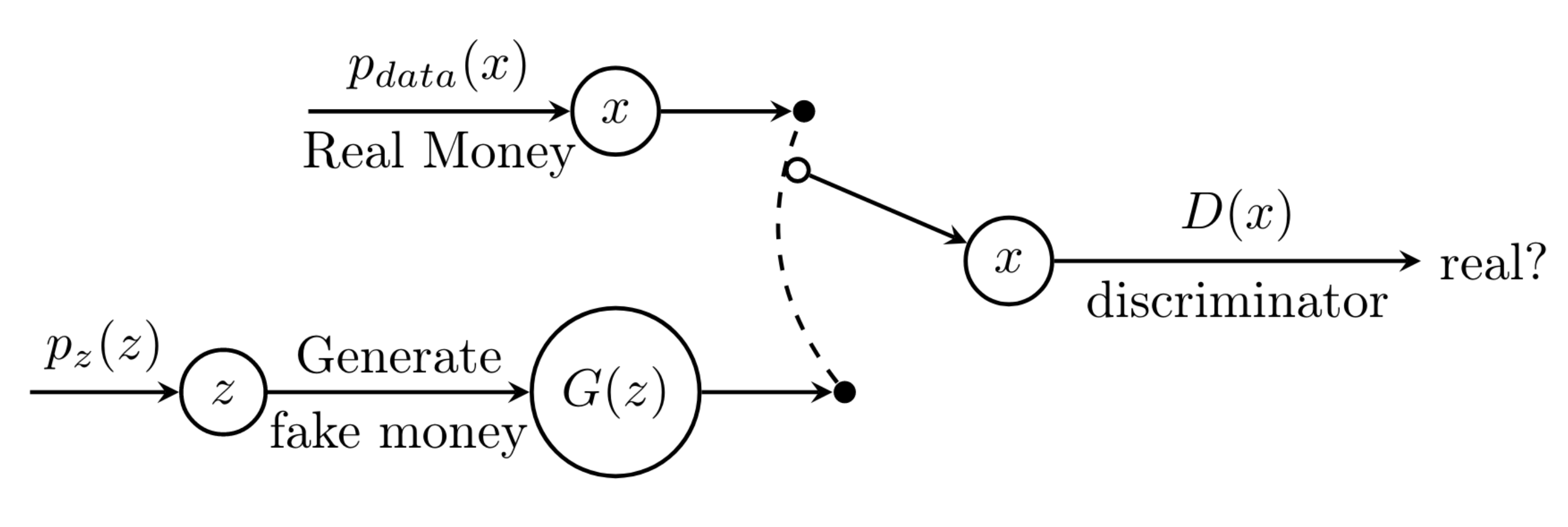
It turns out, yes! We can always find such a function $G$. To build $G$, we will utilize a class of generative machine learning models known as Generative Adversarial Networks.
Can We Use a Simple CNN?
Before considering complicated solutions, first question we should ask is: do we need GANs at all, or will a simple CNN suffice? There exist several generative CNN models—Encoder-Decoder, U-Net, etc.—so why don't we use them?
The problem is as follows: CNNs learn to minimize a loss function, and although the learning process is automatic, we still need to carefully design the loss function. Which means, we need to tell the CNN what we want to minimize!
But if we take a naive approach and tell the CNN to minimize the euclidean distance between the input image and output image, we get blurry images. This happens because it is much "safer" for the L2 loss to predict the mean of the distribution, as that minimizes the mean pixel-wise error.
Rather than specifying a carefully crafted model and loss for each Image-to-Image problem. It would be better if we could specify some goal like: "make the output indistinguishable from reality".
While this may seem like a vague target, this is exactly what Generative Adversarial Networks claim to do!
Enter Pix2Pix
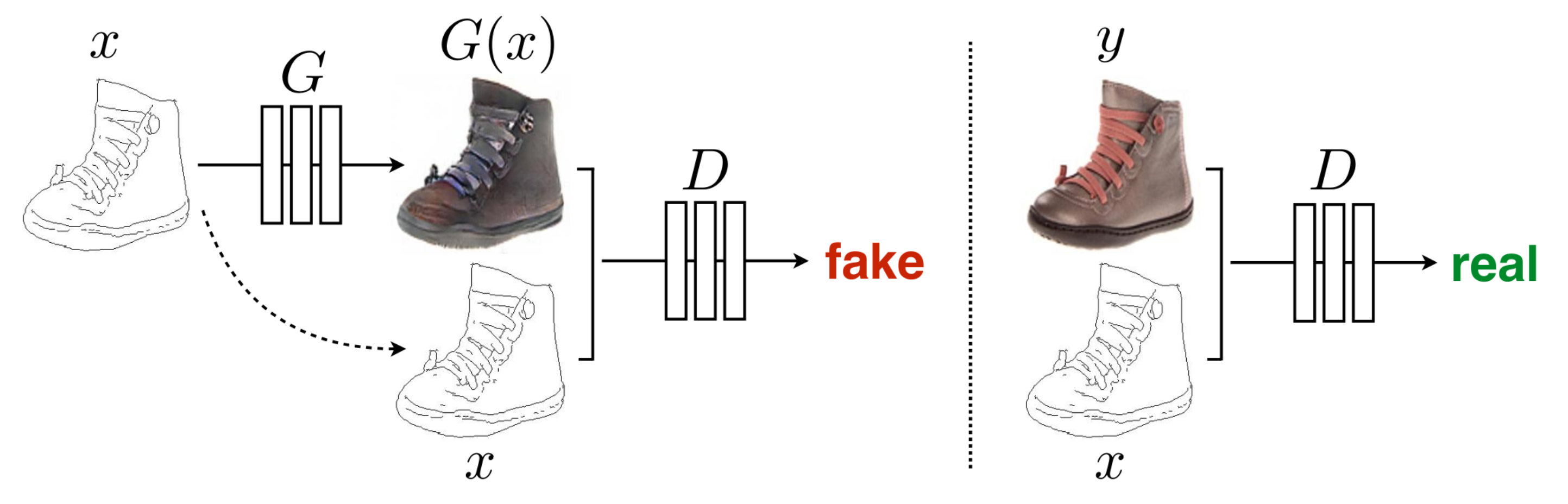
The main idea behind the Pix2Pix paper is to use a Conditional Generative Adversarial Network to learn the loss function, rather than hand-coding a loss function—such as Euclidean distance—between target and input images.
Objective
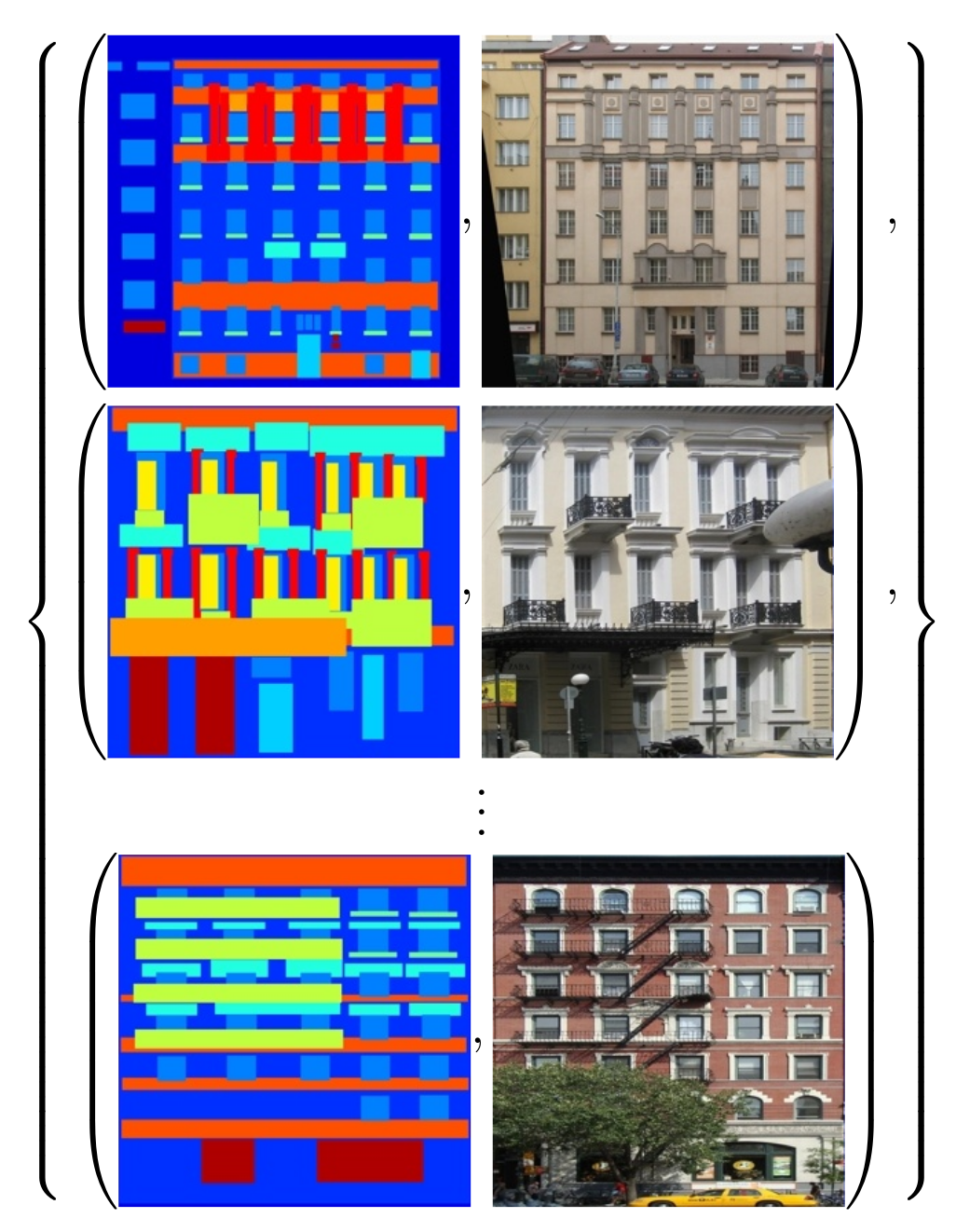
The goal is to generate a target image, which is based on some source image. As we don't want our model to generate random images, we use a variant of GANs called Conditional GANs.
As the name suggests, Conditional GANs take a conditional variable to both the generator $G$, and the discriminator $D$. For example, if we have a training pair $(c, y)$, where we want to generate the item $y$ based on the value of $c$, we pass $c$ to both $G$ and $D$.
The loss function then becomes:
In their experiments they found mixing both the adversarial loss and a more traditional loss—such as L1 loss—was helpful for training the GAN. The loss function for the discriminator remains unchanged but the generator now not only has to fool the discriminator but also minimize the L1 loss between the predicted and target image.
The final objective becomes for the generator becomes:
Where $\lambda$ is a hyperparameter for our model.
Note: For training the generator, instead of providing random noise as a direct input, they provide noise in the form of dropout.
Discriminator Architecture
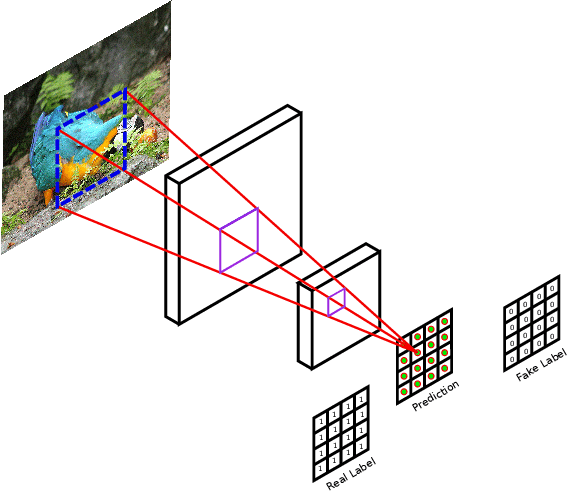
Since we are already adding a traditional loss such as L1(or L2) which—although produce blurry results when used alone—are very useful for enforcing correctness at the low frequency. This is the main idea behind the PatchGAN discriminator.
PatchGAN architecture restricts the discriminator to model only high frequency structure in the generated image. To model this, it is sufficient to restrict the attention to local image patches.
Therefore, rather than generating a single probability in range $[0, 1]$, the discriminator generates a $k \times k$ matrix of values in range $[0, 1]$ where each element in the matrix corresponds to a local patch(the receptive field) of the image.
One advantage of PatchGAN is that the same architecture can extend to images of higher resolution with same number of parameters, and it would generate a similar, but larger, $k' \times k'$ matrix.
Inspired by DCGAN, the discriminator is implemented as a Deep CNN, build up of repetitions of modules of form: Convolution - BatchNorm - ReLU, where we down-sample until we reach the required $k \times k$ matrix, which we then pass through the logistic function to get the elements in range $[0, 1]$.
Generator Architecture
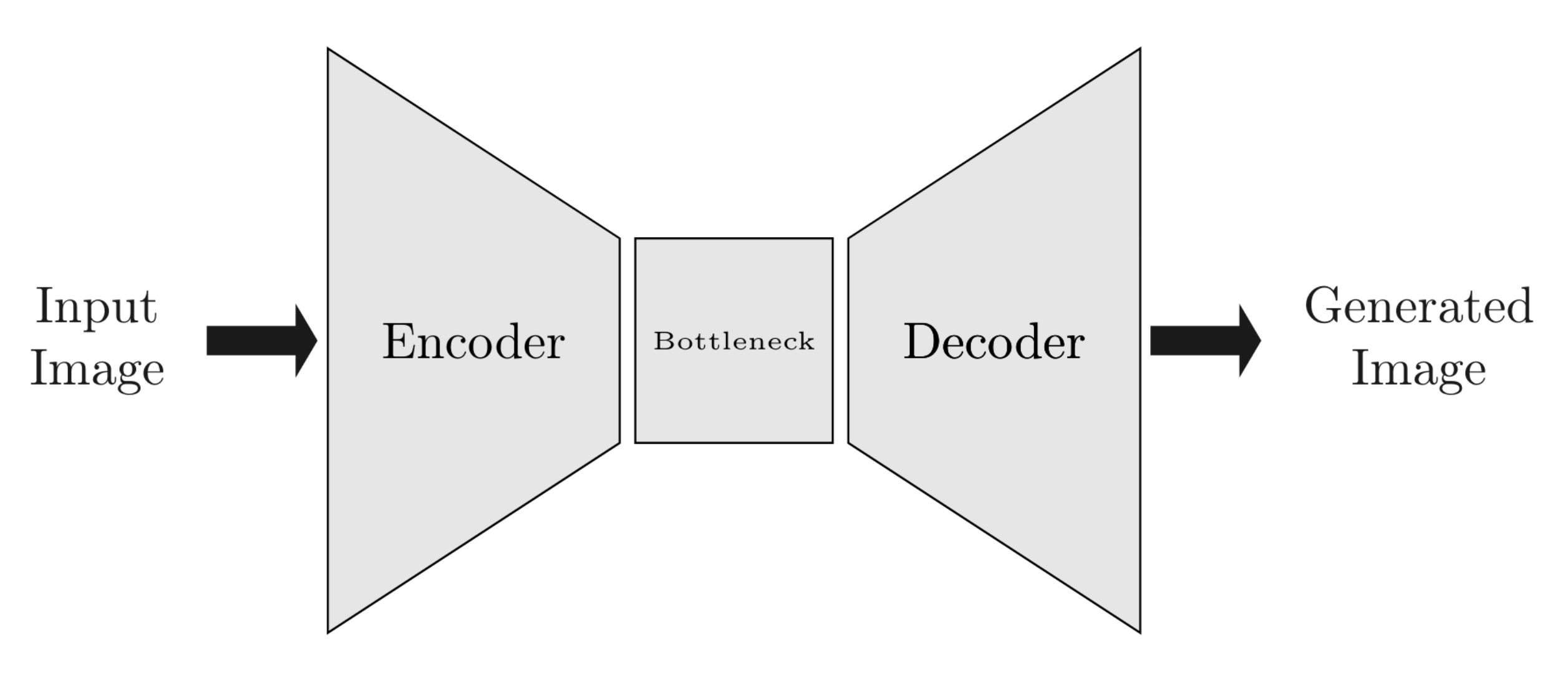
One of the obvious choices for a generator architecture for Image-to-Image translation, is the encoder-decoder network.
In this kind of network, the input image is passed through a series of layers which down-sample the resolution but increases the number of channels until we reach an image of size $1 \times 1$, after that the process is reversed until we reach the resolution of the original image.
Here also we use modules of the form: Convolution - BatchNorm - LeakyReLU for encoder, for decoder we use: TransposeConvolution - BatchNorm - ReLU.
For many interesting image-translation problems, there is a lot of low-level information shared between the input and output image. For example, in the case of colorization, the input and output share the location of edges. To preserve this information, we add skip connections to create a "U-net" like architecture.
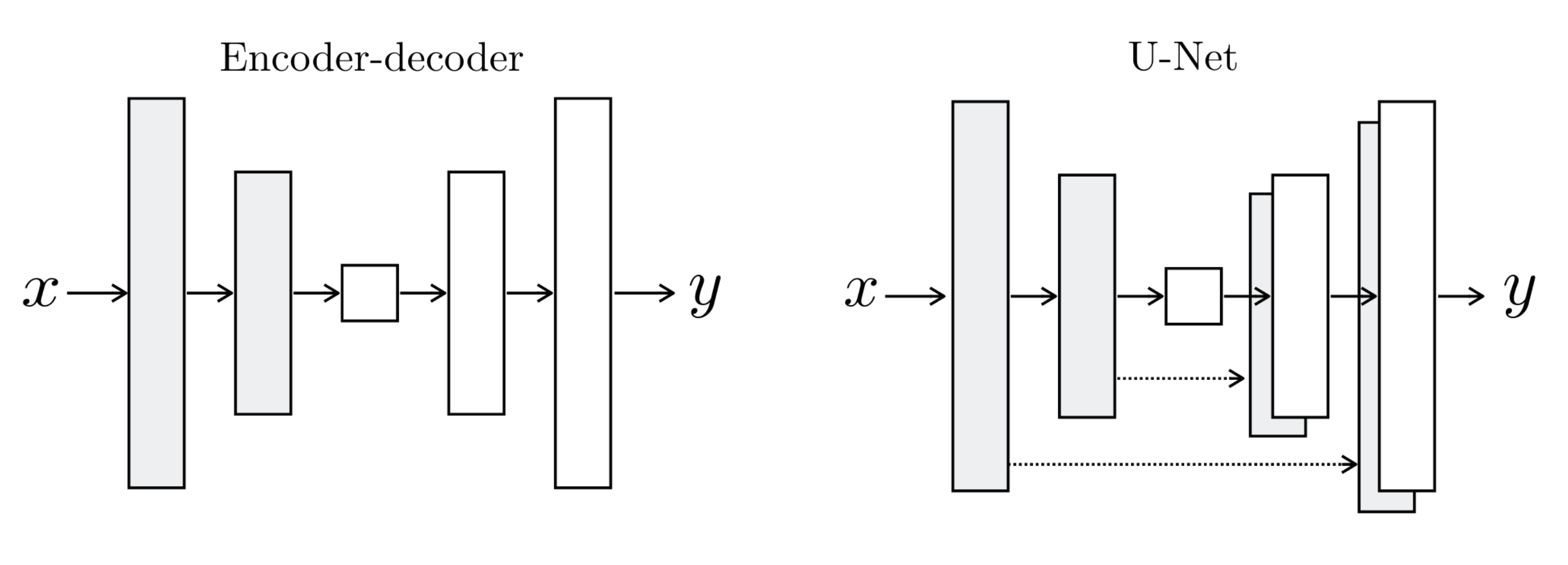
This network is similar to Encoder-Decoder network, but we add some extra skip-connections between layer $i$ in the encoder and layer $n-i$ in the decoder.
Experiments
To demonstrate the versatility of the Pix2Pix approach, I applied the model on three different datasets with seemingly very different problem setting.
The datasets used are: Satellite2Map, Edges2Shoes, and Anime Sketch Colorization.
I used the Adam Optimizer with hyperparameters $\beta_1 = 0.5$ and $\beta_2 = 0.999$. Learning rate was set to $0.0002$, and $\lambda$ used was $100$.
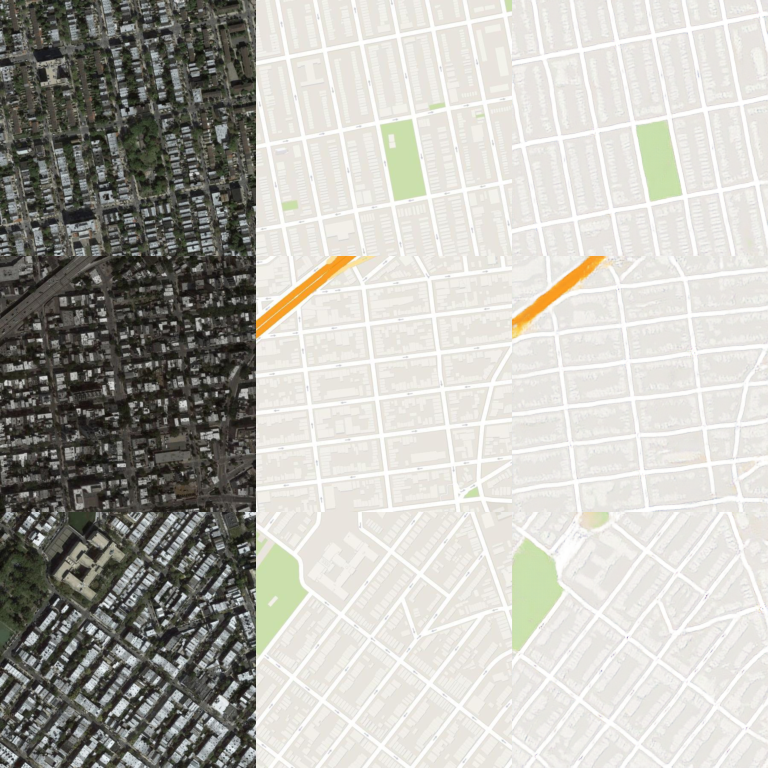
Satellite $\rightarrow$ Map
This dataset consists of paired images of aerial photography and their corresponding map view scraped using google maps. There are $1096$ training images of size $256 \times 256$. The model was trained for $150$ epochs with batch size $1$.
Edges $\rightarrow$ Shoe
This dataset consists of paired images of sketches of shoes and the corresponding actual image (created using edge detection). There are $50$k training images of size $256 \times 256$. The model was trained for $30$ epochs with batch size $1$.

Sketch $\rightarrow$ Colored
This dataset consists of paired images of anime line sketch images and the corresponding colored image. There are $14$k training images of size $256 \times 256$. The model was trained for $75$ epochs with batch size $1$.

References
- Goodfellow, Ian, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. “Generative Adversarial Nets.” Advances in Neural Information Processing Systems 27.
- Isola, Phillip, Jun-Yan Zhu, Tinghui Zhou, and Alexei A Efros. 2017. “Image-to-Image Translation with Conditional Adversarial Networks.” In Proceedings of the Ieee Conference on Computer Vision and Pattern Recognition, 1125–34.